Как пользоваться
таблицей Брадиса?

Давайте на нескольких примерах посмотрим как пользоваться таблицей Брадиса.

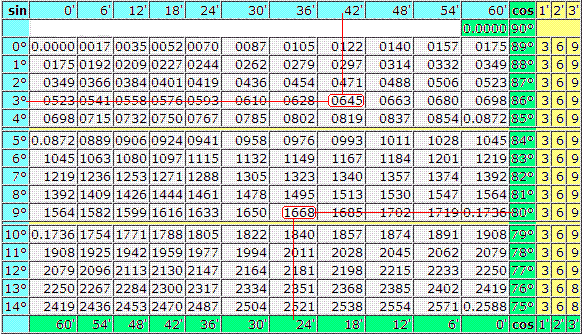
sin 7°=0.1219     косинусы смотрим снизу   cos 82°=0.1392 надеюсь это понятно.
sin 3°42′=0.0645 на картинке красным цветом cos 80°24′=0.1668 то же просто

Хочу заметить все тоже самое верно и для определения значений
тангенсов и котангенсов.

Теперь возьмем более сложный вариант, если угол представленный в таблице отсутствует, то следует выбирать наиболее близкое к нему значение (из имеющегося в таблице синусов и косинусов), а на имеющуюся разницу, которая может быть 1′,2′,3′, взять поправочное значение из желтой графы, как показано в примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 или
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654

Так же необходимо запомнить правило, для синуса поправка имеет положительный знак, а для косинуса отрицательный
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 или
cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659

Оказывается пользоватся таблицей Брадиса не так уж и сложно. Надо еще раз очень внимательно все посмотреть, попробовать, и можно смело браться за самостоятельные расчеты.